The following programs are generally
listed according to the speed at which they compute values of Pi. (The
last one listed here being the fastest program!)
Since I'm running Windows 95/DOS 7 on a PC,
each program listed here is at least available in an x86 (PC) DOS (or
Win32) binary form. Executables for a particular program on another
platform may exist, since some of them come with their own open
source code! (Consult the program homepages and links listed below.)
1) The easy to run Super_Pi
(for MS-Windows™)
by Yasumasa Kanada
Download Super_Pi
now (in a 72 kb .zip file) and Calculate up to 32 Million digits of Pi.
There are twelve different digit-lengths to choose from (see below). Simply
extract the files (Super_pi.exe,
Super_pi.hlp and
Super_pi.txt) into any directory
and run the program. The program creates the file pi_rec.txt to keep track of which sizes you've
calculated, and the digits are placed into a file called
"pi_data.txt"
(CAUTION: Each time you
calculate a different length of Pi, this file will be overwritten! So rename the file if you want to
keep those digits.)
When the program starts, you'll see a window like this: |
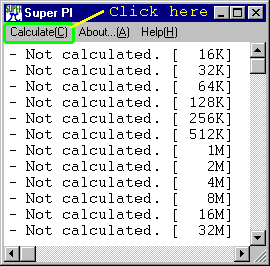 |
When you begin a calculation, a " Stop (S) " item will appear on the Menu so you can abort any runs you accidentally started or that are taking too long.
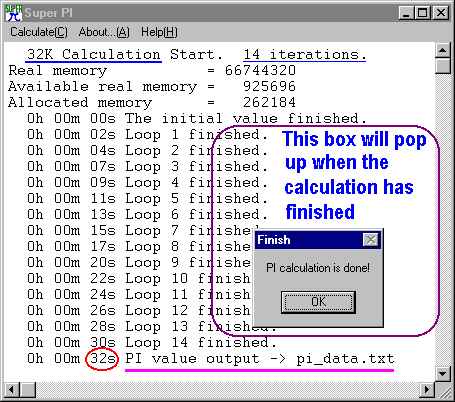
The following pic shows a full run to calculate just 32,768 digits ( the
32K choice) on a 100MHz PC. Time shown: 32 seconds; that's exactly 1024
digits/sec (not very fast). Calculating 512K, took 11m 06s, so the speed
went down to only about 787 digits/sec; even worse! You could probably D/L
large files of Pi from the Net faster than trying to calculate them on an
old computer (less than 300 MHz CPU) with this program; especially if you
download those files with over 50% .zip compression.
 |
2) pi-AGM (Arithmetic Geometric Mean Program) by Carey Bloodworth
Check out Carey's Home Page and detailed math descriptions
of subroutines that help you build a fast Pi program here:
http://www.bloodworth.org/.
3) pi_fft5 (pi_css5) by Takuya Ooura
4) PiFast33 by Xavier Gourdon
5) QPI-Quick Pi by Steve Pagliarulo
![]() Download: qpi10.zip
(only 44kb) Read: QuickPi.txt
Download: qpi10.zip
(only 44kb) Read: QuickPi.txt
A
Win 32 console program for i386 or above (PC) computers.
Steve's program is somewhat faster than Xavier Gourdon's; if you keep the number of digits under 8 million (this crossover point may vary a bit for different machines), and eight (8) times faster than that of Kanada's Super_Pi for a 512Kb run!
Besides computing Pi, by adding either the parameter -2 or -e to the command
line, this program can also carry out the square-root of 2 (using Newton's
iteration method) or compute e (using the series SUM of 1/n!).
For Pi itself, the program can use the following formulas: one from the
Chudnovsky brothers [default], a Gauss-Legendre AGM [-a], the Brent-Salamin
AGM [-s], or a quartic from the Borwein brothers [-b].
Program usage: qpi [digits] [-2|-e|-a|-s|-b]
Steve included the other Pi methods for verification or comparison purposes, the default (Chudnovsky) is always the fastest of the four! On my old 100MHz machine, I got the following times when calculating 524,288 digits of Pi:
default (Chudnovsky brother's Equ.) = 83.29 seconds
-a (Gauss-Legendre AGM) = 170.61 seconds
-s (Brent-Salamin AGM) = 209.32 seconds
-b (Borwein brother's Quartic) = 257.95 seconds
Note: For the calculations above...
The Default method -> Has to compute only: 524,295 Digits
But, the Gauss-Legendre AGM -> Has to compute: 715,319 Digits
using 18 Iterations,
the Brent-Salamin AGM -> Has to compute: 1,011,616 Digits
using 19 Iterations and
the Borweins' Quartic -> Has to compute: 715,319 Digits
using 9 Iterations.
However,
These other methods must not be actually calculating Pi out to
these other digit lengths fully as you might surmise, because:
Although asking qpi to calculate 1,011,600 digits using -s
(the Brent-Salmin AGM) does reveal that it will be computing
only 1,011,616 digits to do so, it still took 413.04 seconds
to complete the the calculations. Whereas, the Default method
(Chudnovskys' formula), which computed 1,011,605 digits took
only 182.21 seconds!
As you can see, Steve listed the other methods in his usage
statement in the order of their speeds (-a, -s, -b).
qpi.exe defaults to "Chudnovskys' formula" for Pi when you enter only "digits" values. You must redirect the output (using ">") if you want to save it to a file, for example:
C:\thestarman3\math\pi\QuickPi>qpi > pi.txt
will create the following lines in pi.txt:
QPI-Quick Pi v1.0, (c) 2000 S. Pagliarulo Address comments to: s_pagliarulo@hotmail.com usage: qpi [digits] [-2|-e|-a|-s|-b] 400 digits of pi using Chudnovskys' formula Series size : 29 (411 Digits) Series computation time : 0.01 Final value computation time : 0.01 Total time : 0.05 seconds Pi = 3. 1415926535 8979323846 2643383279 5028841971 6939937510 : 50 5820974944 5923078164 0628620899 8628034825 3421170679 : 100 8214808651 3282306647 0938446095 5058223172 5359408128 : 150 4811174502 8410270193 8521105559 6446229489 5493038196 : 200 4428810975 6659334461 2847564823 3786783165 2712019091 : 250 4564856692 3460348610 4543266482 1339360726 0249141273 : 300 7245870066 0631558817 4881520920 9628292540 9171536436 : 350 7892590360 0113305305 4882046652 1384146951 9415116094 : 400
You always get a layout of 50 digits per line in 10-digit groups with a " : sum" at the end of each line giving the total digits of Pi up to the last digit in that line. There's no way to change the layout as you can with Gourdon's PiFast program.
This page is still under
construction... I plan on adding descriptions and displays of sample runs for
each of these Pi programs and other unique ones as I discover them!
To contact me, use my:
Feedback page
here. (©2001 by Daniel B. Sedory)